Improving CFD Predictions Using Sparse Data
Computational fluid dynamics (CFD) is widely used to analyze turbulent flows, but often faces a trade-off between computational cost, modeling complexity, and the accuracy of results. Our research employs data assimilation of sparse reference data to correct closure terms in transport equations, thereby enhancing the results of coarsely resolved turbulent flow simulations.
Turbulent flows are ubiquitous in engineering applications and in nature. While they can be studied based on analytical analyses and experiments, turbulent flow simulations are an important tool in research and engineering. Such simulations always involve a trade-off between computational cost, modeling, and accuracy of results. Direct solution of the Navier-Stokes (DNS) equations is only feasible for academic studies and requires considerable computational resources. Large eddy simulations (LES) model the subgrid scale stresses while resolving much of the turbulent motion. However, for many applications, the computational cost of LES is still too high and the Reynolds-averaged Navier-Stokes (RANS) equations are used to model turbulent flows. Although they are an established tool, they provide only averaged quantities and rely heavily on closure models with limited applicability.
Our goal is to improve the accuracy of coarse-resolution, low-cost turbulent flow simulations through stationary data assimilation of sparsely distributed reference data. First, an approach based on the stationary discrete adjoint method was developed to assimilate averaged reference velocity data in RANS simulations based on the modification of the eddy viscosity field. Then, the method was further developed for application in hybrid RANS/LES, URANS and LES simulations and for a forcing term correcting the Reynolds stresses. Critical components such as the parameter regularization, the optimization method, the mapping of the optimization parameters as well as the placement of the reference data locations were investigated.
Eddy Viscosity Tuning
While classical eddy-viscosity closure models for the Reynolds-averaged Navier-Stokes (RANS) equations provide good results for a wide range of flows, they still suffer from inaccuracies. In a first work [external page Brenner, Piroozmand, Jenny, Journal of Computational Physics, 2022] we corrected eddy viscosity fields initially obtained from a k-ε model with a spatially variable corrective field.
In particular, sparsely distributed averaged LES reference velocity data from the literature was assimilated using a stationary variational data assimilation approach based on approximate cost function gradients. Due to appropriate regularization, smooth parameter fields were obtained and the resulting RANS velocity results agreed well with the reference data, specifically also in the recirculation zone of the periodic hill setup, where the uncorrected turbulence model showed some deviations.
PLDR Regularization
While the initial results for the assimilation of free stream velocity reference data provided encouraging results, the assimilation of near-wall data proved to be difficult. Hence, an improved regularization approach based on a piecewise linear dimensionality reduction (PLDR) was introduced [external page Piroozmand, Brenner, Jenny, Journal of Computational Physics, 2023] to not only reduce the number of parameters, but also provide more physical parameter fields. In addition to correctly reproducing the mean shear-flow in RANS, the PLDR regularization makes it possible to obtain correct wall shear stress profiles through data assimilation.
Hybrid RANS/LES
Next, the eddy viscosity based data assimilation method was extended to the hybrid RANS/LES framework [external page Piroozmand, Brenner, Jenny, Theoretical and Computational Fluid Dynamics, 2024] originally introduced by Xiao and Jenny [external page Journal of Computational Physics, 2012]. The approach is based on the assimilation of sparse wall shear stress data with the goal of obtaining accurate average velocity fields and wall shear stress profiles. It was shown that the proposed approach outperforms both the original hybrid RANS/LES framework and standalone sparse wall-data assimilated RANS models.
Corrective Forcing
While the eddy viscosity correction based data assimilation provides good results for the well-resolved periodic hill setup, it incurs relatively high computational cost due to the required number of simulation evaluations. This cost can be reduced by using less well resolved meshes, but negative effects on the overall performance have been observed. Further, due to the Boussinesq hypothesis, the parameter can only influence the flow where there is a sufficiently large velocity gradient, and a parameter mapping is required to prevent numerical instabilities due to negative viscosity values.
To address these issues, the data assimilation framework has been extended by introducing a corrective forcing for the Reynolds stress tensor, instead of tuning the eddy viscosity [external page Brenner et al., Computer Methods in Applied Mechanics and Engineering, 2024]. Using the Helmholtz decomposition, this corrective forcing term can be represented by a scalar and a vector potential field. If only velocity reference data are assimilated, only the vector potential field is of relevance, while the scalar potential field is absorbed in the modified pressure. In the case of two-dimensional simulations, only the third component of the vector potential field is needed, and used as the parameter for data assimilation.
The results indicate a superior performance of this approach over the original eddy viscosity correction approach and a naive direct assimilation of the eddy viscosity. In addition, the computational cost has been significantly reduced by using coarser mesh resolutions, improved optimization methods, and the fact that the method does not require parameter mapping.
Mean Flow Data Assimilation
In a subsequent study, data assimilation is used to mitigate discrepancies in the modeled divergence of residual or Reynolds stresses in LES (see [external page Plogmann, Brenner, Jenny, arXiv, 2024]) and URANS (see [external page Plogmann, Brenner, Jenny, Computer Methods in Applied Mechanics and Engineering, 2024]) simulations, respectively. Recognizing the challenges posed by the computational cost of four-dimensional variational (4DVar) data assimilation for unsteady flows, a three-dimensional variational (3DVar) data assimilation scheme is proposed. After time averaging the unsteady momentum equations, the stationary discrete adjoint method can be used. A stationary corrective forcing term is introduced into the unsteady momentum equations and iteratively updated within the gradient-based optimization framework in conjunction with the adjoint gradient. The effectiveness of the proposed framework is demonstrated for turbulent flow over periodic hills and around cylinders of various shapes. Coarse meshes are used to further improve the speed of the optimization procedure. The results show that the adjoint-based assimilation of averaged velocity data enables the optimization of mean flow, vortex shedding frequency (i.e. Strouhal number), and turbulent kinetic energy (for LES).
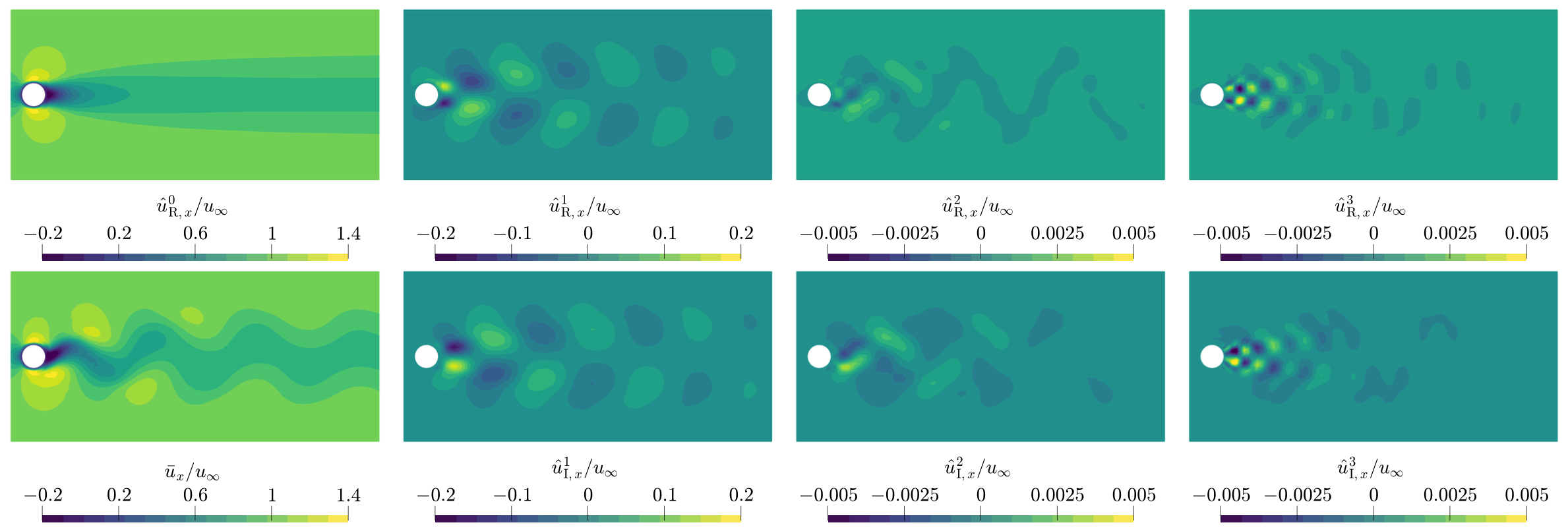
Assimilation of Fourier Mode Data
To overcome some of the limitations of mean flow data assimilation and to further optimize the flow dynamics, Fourier transformed velocity data are assimilated. To do this, the URANS equations are solved in physical space and time, and a discrete-time Fourier transform is performed assuming a flow with time-periodic statistics. Therefore, the corresponding discrete adjoint equations are stationary, and the data are assimilated in the Fourier domain. As a data assimilation parameter, an unsteady divergence-free source term is added to the URANS equations to correct for discrepancies in the closure model. Since this unsteady parameter is expressed by a Fourier series expansion, it is represented by the (stationary) Fourier coefficients in the Fourier domain with respect to the Fourier mode of interest. Although time-resolved data are still needed to obtain Fourier-transformed reference data, time-stepping schemes in a dynamic data assimilation framework (e.g., 4DVar) do not need to be employed. It was shown that for coarse URANS simulations, sparse Fourier-transformed (velocity) reference data can be assimilated by a 3DVar approach, avoiding the use of the very costly 4DVar method. Furthermore, a standard fluid solver (here based on a finite volume method implemented in OpenFOAM) is used and a harmonic solver is avoided, making this method an attractive tool for more complex flows [external page Plogmann, Brenner, Jenny, Physics of Fluids, 2024].