Markovian Velocity Process Model
Daniel W. Meyer, Patrick Jenny, Hamdi Tchelepi (Stanford University)
Abstract
Groundwater is stored in large porous rock formations called aquifers and may be exposed to contamination, for example, by leaking storage sites of chemicals or nuclear deposition sites. Simulation tools are needed for groundwater management decisions, for example, dealing with the coordination of remediation actions in the wake of a contamination hazard. Rock formation characteristics that determine groundwater flow, however, are typically spatially heterogeneous and are hardly accessible. Consequently, these characteristics are subject to large uncertainties. In this context, we are developing a simulation approach that is conceptually similar to the PDF methods applied for the simulation of turbulent flows. It is applicable for formations of different heterogeneity levels at very low computational costs.
Subsurface Flow and Transport
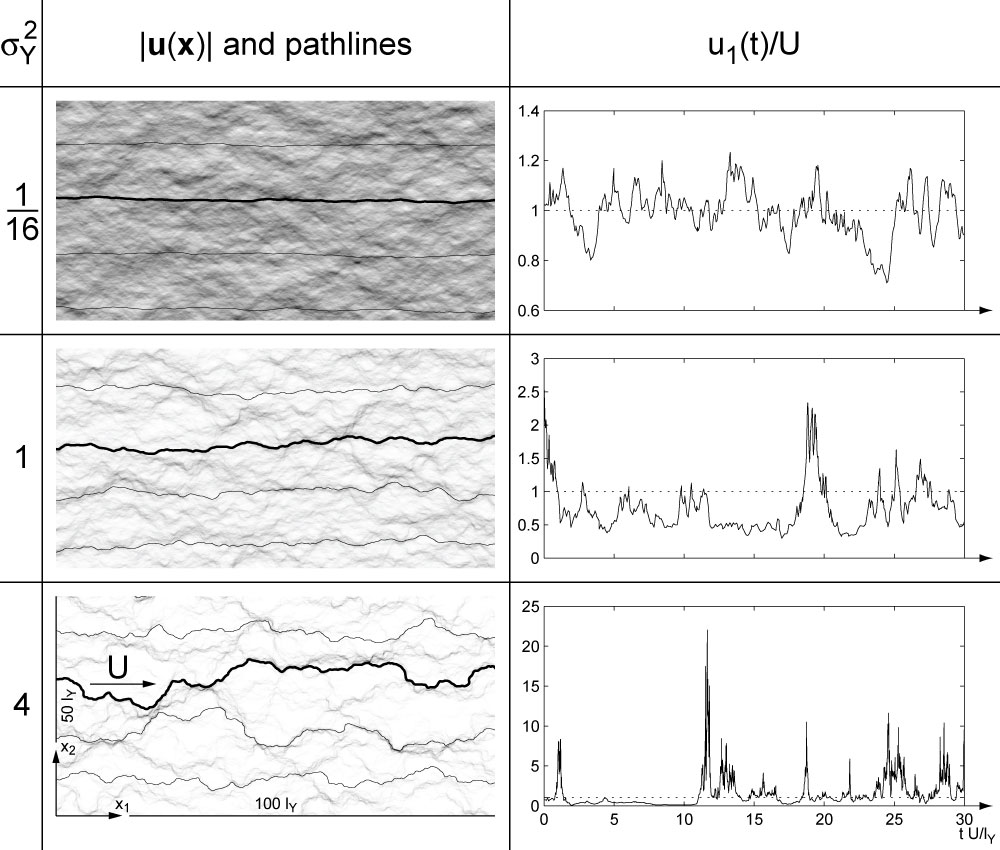
The flow of groundwater in the porous subsurface is described by Darcy's law, which linearly relates the flow rate vector with the local pressure gradient. The flow rate magnitude depends as well linearly on the hydraulic conductivity, which describes how easily water can flow through the pores. To describe the water flow, we focus on a Lagrangian description that is well suited to investigate the transport of tracers or contaminants. The figure gives an impression of the Lagrangian velocity dynamics as a function of the heterogeneity level of the hydraulic conductivity.
Uncertainty Assessment
Due to the heterogeneity and the induced uncertainty mentioned in the general description, the conductivity is modeled as a random field by means of geostatistical models. Accordingly, different permeability distributions and transport pathlines are probable. To quantify the resulting uncertainty in the flow and transport behavior for a given geostatistical aquifer model, typically sampling over different probable conductivity maps is done (Monte Carlo (MC) simulation). Here, a large number of flow and transport problems have to be solved, which makes this approach computationally demanding.
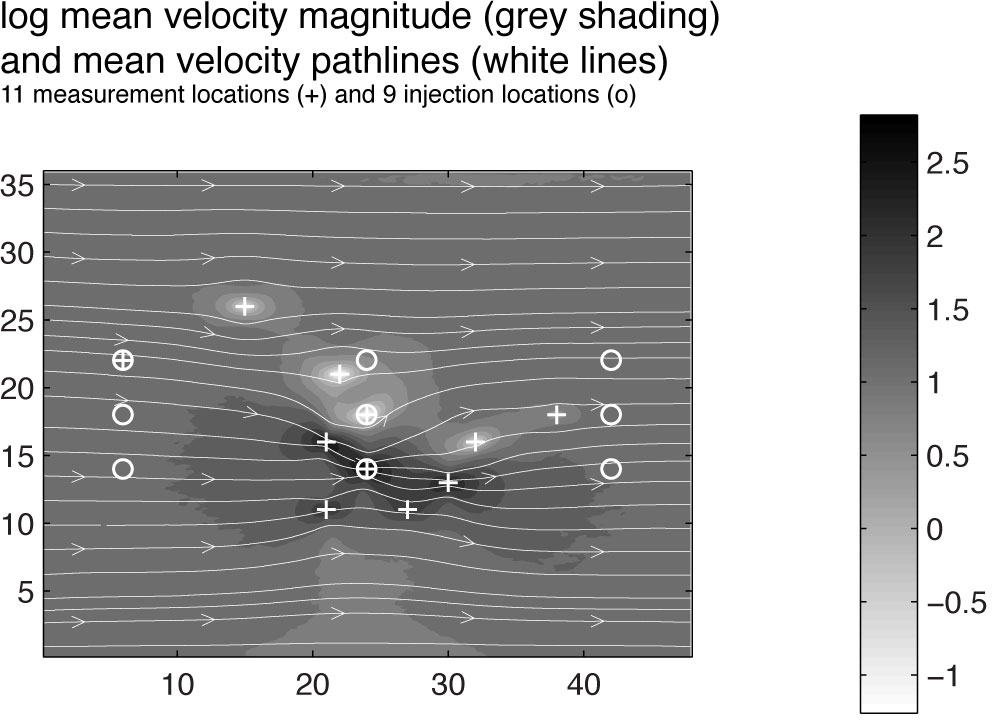
We propose to replace the ensemble of probable flow fields or transport pathways by a stochastic Lagrangian velocity process or more precisely Markovian velocity process (MVP). Our process parametrization accounts for the local conductivity heterogeneity level and mean flow trends that result from available conductivity measurements. An example of how conductivity measurements effect the mean flow pattern is given in the figure.
Markovian Velocity Process Model
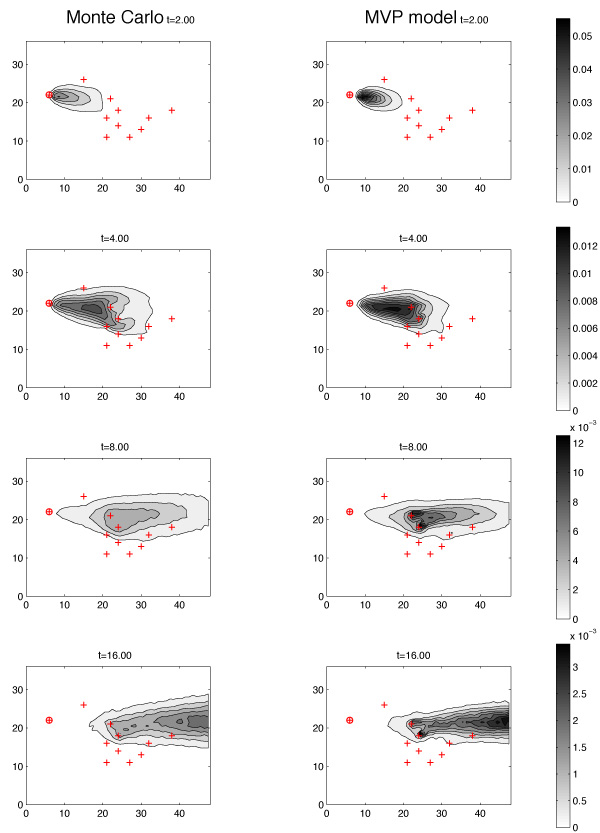
An example where transport statistics resulting from the MVP model are compared with conventional MC reference simulations is provided in the figure below. In the depicted scenario, tracer was released from the indicated red circle at time t = 0. The normalized mean contaminant concentration is plotted at different non-dimensional times t. Even though there are minor differences between the model predictions and the MC reference results it has to be pointed out that the model results were obtained at a tiny fraction of the simulation time required for the MC results (several days of computing time). More precisely, an MVP model run was approximately 1000 times faster than a MC reference simulation.
Read more ...
- external page D. W. Meyer, P. Jenny, and H. A. Tchelepi. WRR, 46(12), 2010.
- external page D. W. Meyer and H. A. Tchelepi. WRR, 46(11), 2010.
- external page D. W. Meyer, H. A. Tchelepi, and P. Jenny. WRR, 49(5), 2013.
- external page D. W. Meyer and F. Saggini. Phys. Rev. E, 93, 2016.
- external page S. Dünser and D. W. Meyer. AdWR, 92, 2016.
- external page D. W. Meyer. AdWR, 105, 2017.
- external page D. W. Meyer. AdWR, 121, 2018.