Flow in Porous Media

Flow and transport in porous media has many applications in earth science, energy science, and many other areas. Examples in which we are interested are oil and gas recovery, CO₂ storage in geological sub-surface formations, geothermal power exploration, and uncertainty assessment of flow and transport.

Numerical Modeling of Fluid-Injection-Induced Shear Failure

Geothermal reservoir simulation represents a multi-physics problem involving for example fluid flow interacting with geomechanics. In this project, a numerical modeling framework is developed, which is suited to study induced seismicity due to reservoir operation. Both shear failure, due to fluid injection into fractured reservoirs [external page Deb and Jenny 2017], as well as the microseismic effect of fracture-aperture changes are modeled. The flow problem is solved for both fractures and porous damaged matrix. A grid- and timestep-independent numerical method was developed for flow and mechanical failure in fractured reservoirs [external page Deb and Jenny 2017 and external page 2020]. Read more

Simulation of Fractured Geothermal Reservoirs

This is an interdisciplinary collaboration with various earth scientists from ETH Zürich. In the context of geothermal power production, Karvounis, Hajibeygi, and Jenny [external page 2011 and external page 2016] have created a modeling framework for flow and transport in fractured porous media. It has proper interfaces which allow to interfere with rock mechanics and rock chemistry models. Moreover, everything is coupled with heat conduction in the rock. Due to the very large number of fractures, only the large ones are resolved. The cloud of small fractures is treated by effective permeabilities.

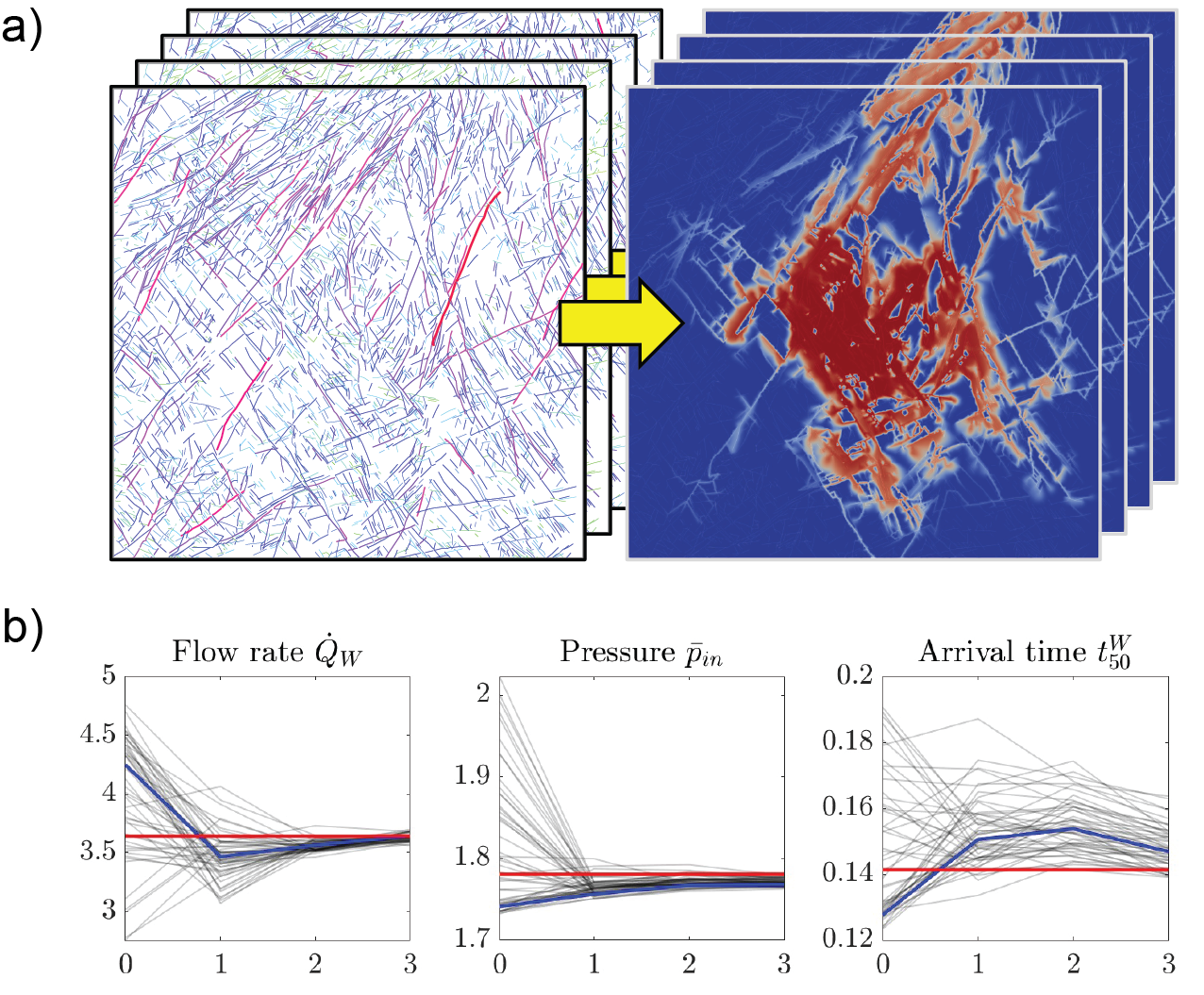
In a second collaborative effort involving Prof. Stephan Matthai (University of Melbourne), the uncertainty in the reservoir or more precisely the highly conductive fractures is addressed. To this end, we start from an ensemble of prior reservoir scenarios or realizations and update their parameters based on pressure and flow rate measurements becoming available over time during the stimulation-phase of a geothermal reservoir. For parameter updates, we use the ensemble Kalman filter (EnKF) methodology. After the initial stimulation phase, EnKF parameter updates are continued by using tracer measurements leading eventually to a posterior ensemble with significantly reduced parameter uncertainties [external page Liem and Jenny 2020].

Application of the EnKF to flow/transport in fractured geothermal reservoirs — Application of the ensemble Kalman filter (EnKF) to flow and transport in fractured geothermal reservoirs. In panel a) an ensemble of fracture realizations with different parameters is depicted together with the resulting tracer concentration fields (tracer is injected at the center, red and blue correspond to high resp. low concentrations). In panel b) the reduction of the parameter uncertainty resp. the resulting uncertainty in key flow and transport quantities is depicted over consecutive EnKF iterations (x-axis). Each grey line represents a fracture realization and the blue line the ensemble mean as they all approach the reference values corresponding to the true reservoir (red lines).

Uncertainty Assessment of Flow and Transport in Porous Media

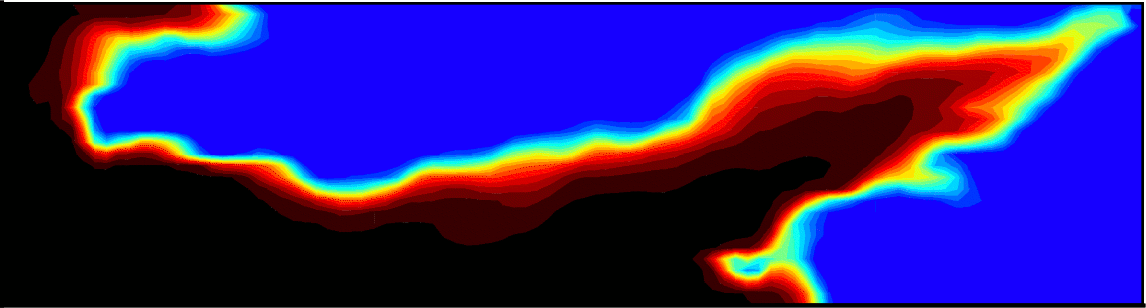
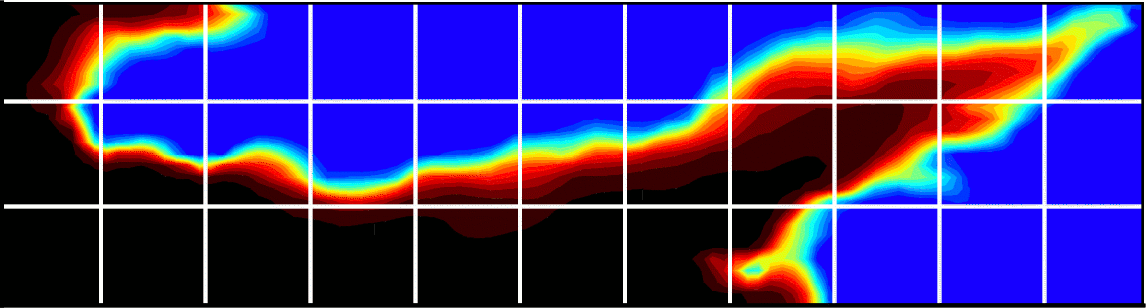
The transport of chemical substances in the subsurface is relevant in many different applications. For example, for the assessment of nuclear waste deposition sites or for the coordination of remediation actions after a contamination hazard, predictive simulation tools are required. These tools have to account for the uncertainty in the soil parameters, since measurements of the subsurface structure are typically very scarcely available. The main goal is to develop a simulation framework for tracer flow and transport that provides probabilistic information about local tracer concentration evolutions.

In this context, a probability density function (PDF) method was developed together with Prof. Hamdi Tchelepi (Stanford University) that is applicable for highly heterogeneous porous media [Meyer, Tchelepi, and Jenny external page 2010a, external page 2010b, and external page 2013, external page Meyer and Saggini 2016, external page Dünser and Meyer 2016, and Meyer external page 2017 and external page 2018]. It accounts for advective transport, pore-scale dispersion, and can incorporate upscaled chemical fluid-phase reactions. Read more

Moreover, in a collaborative effort with Prof. Christoph Schwab and Prof. Siddhartha Mishra (both SAM, ETHZ), a multi-level Monte Carlo method has been developed, which allows to combine expensive high fidelity methods with cheap approximate solvers to achieve output statistics more efficiently [Müller, Jenny, and Meyer external page 2013, external page 2014, and external page 2016]. Furthermore, Müller, Jenny, and Meyer [external page 2011] have devised a combined polynomial-chaos/Monte Carlo method for transport uncertainty quantification.

Prediction of Non-Equilibrium Multi-Phase Flow

Currently, storing CO₂ in geological sub-surface formations seems to be one of the most promising feasible technologies to stabilize the CO₂ concentration in the Earth’s atmosphere. The prime objective of our research is to improve our understanding of how the physics and dynamics at the pore scales is linked to the macroscopic equations, which deal with average values. Therefore we have devised a new Lagrangian framework, which facilitates the formulation of models for sub-Darcy-scale physics [external page Tyagi et al. 2008] and [Tyagi and Jenny external page 2011a and external page 2011b].

At the pore scale, Khayrat and Jenny [external page 2016, external page 2017a, and external page 2017b] have developed simulation capabilities and a sub-phase modeling approach both providing a better understanding of pore-scale multi-phase dynamics.

Multi-Scale Modeling

This is a collaboration with Dr. Seong Lee (Chevron). One of the major challenges in macroscopic simulations is the correct treatment of complex permeability distributions with strong variations and many length scales. To deal with this issue, various upscaling and multi-scale methods have been developed. In collaboration with the company Chevron we devised and developed a new multi-scale finite-volume (MSFV) algorithm, which has several advantageous properties compared with previous multi-scale methods [Jenny, Lee, and Tchelepi external page 2003 and external page 2006], [external page Tchelepi et al. 2007], [external page Lunati et al. 2011] and [external page Hajibeygi and Jenny 2011]. The MSFV method allows for very efficient studies of realistic multi-phase flow scenarios in heterogeneous porous media.

Cortinovis and Jenny [external page 2014] have investigated how the robustness with regard to permeability contrast/variance can be improved by an appropriate enrichment of the coarse space.

Water saturation fine-scale solution — Water injection into oil reservoir. Fine scale solution for water saturation (2673 cells).

Water saturation MSFV — Water injection into oil reservoir. MSFV solution for water saturation (33 coarce cells, 2673 fine cells).