Covid-19 Research
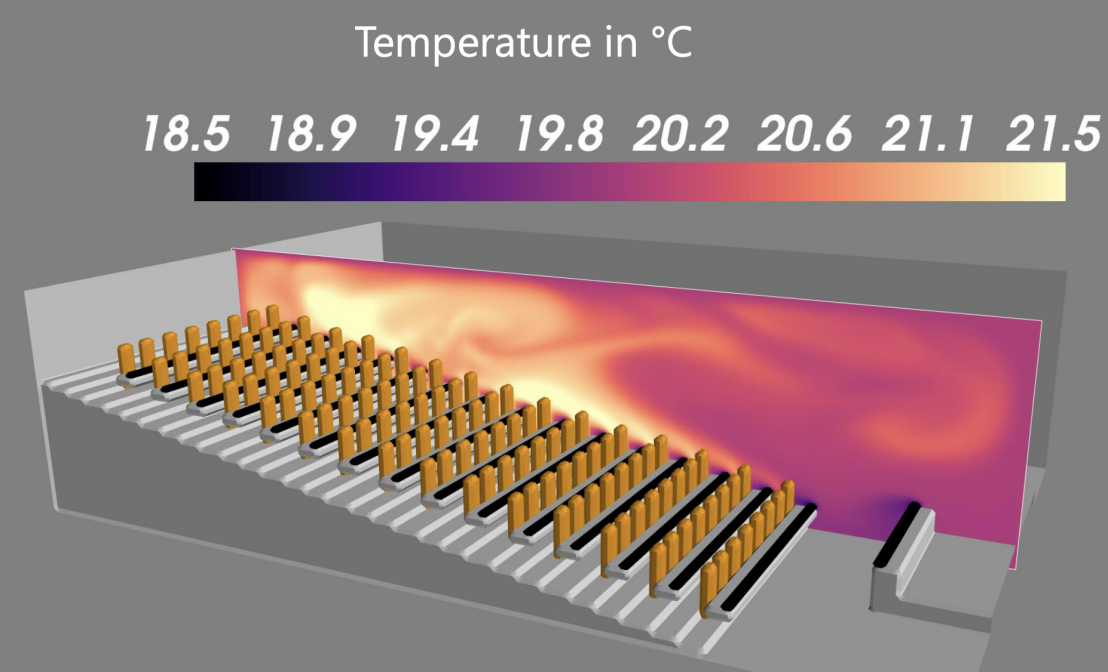
In a short-term development effort, a Navier-Stokes solver with Boussinesq approximation for buoyancy-effects has been implemented in Python to simulate tracer dispersion in lecture halls (see figure). Computationally intense operations have been parallelized using GPUs and PyTorch objects. Thanks to the solver’s implementation, being tailored to the target application, parameter studies including different ventilation systems, lecture hall geometries, and occupation scenarios can be simulated efficiently. The resulting data serves ETH’s coronavirus task force in their decision making process.
Population-balance simulations based on coupled ordinary differential equations have been applied to evaluate different Covid-19 mitigation strategies [external page Gorji et al. 2020a and external page 2021]. Our approach illustrates the merit of mass testing and isolation of identified individuals without or in combination with social distancing. Furthermore, our mathematical model helps to find an optimal balance between different mitigation strategies (incl. repetitive mass testing) to reduce the societal and economic toll of the pandemic and to avoid drastic measures such as lockdowns. In an accompanying work, we have studied the specific benefit of a targeted testing strategy, which is focused on individuals with frequent social contacts [external page Gorji et al. 2020b].