Numerical Simulations of Rarefied Gas Flows
Stephan Küchlin, Patrick Jenny
Abstract
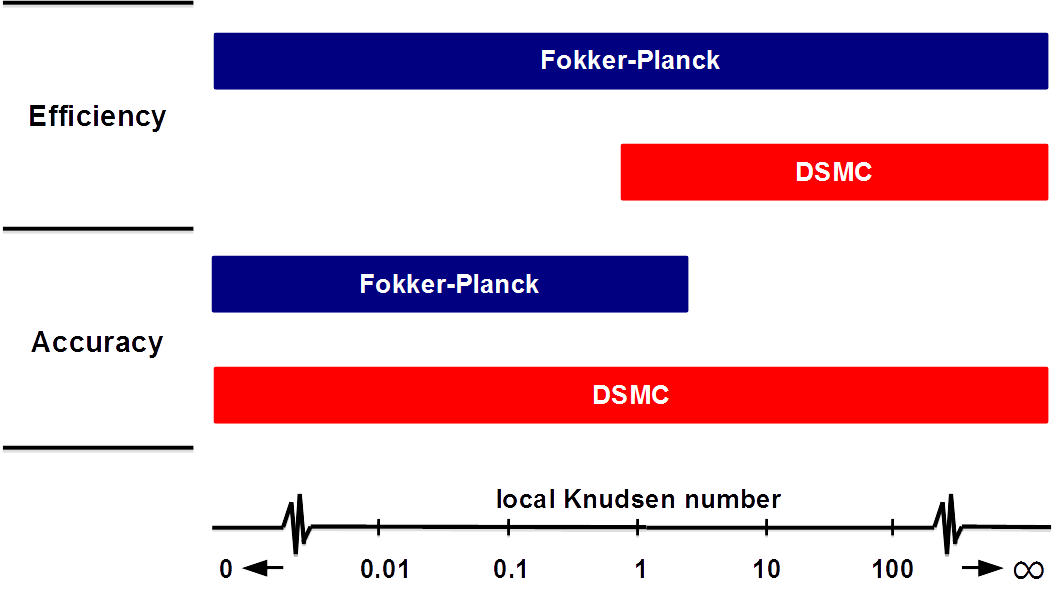
Fluid-flows covering a wide range of Knudsen numbers (Kn) arise for example in space vehicle thrusters or at vehicle reentry. (Kn is defined as the ratio of molecular mean-free path to a relevant flow length scale.) With the Navier-Stokes-Fourier equations no longer valid, the Boltzmann equation is the appropriate mathematical description for rarefied gas flows. It is typically solved numerically by the direct simulation Monte Carlo (DSMC) method. DSMC delivers accurate results but its computational cost becomes large in the near continuum range where Kn is small. The Fokker-Planck (FP) method mitigates this problem as it is efficient at low to moderate Kn, but becomes inaccurate for very large Kn (see figure below). Because both DSMC and FP are particle methods, they may be seamlessly coupled to form a hybrid FP-DSMC method, which allows for efficient and accurate simulations of rarefied gas flows at all Kn.
Stochastic Simulation of the Boltzmann Equation
The Boltzmann equation describes the evolution of the fluid density in the position-velocity phase space under the influence of binary molecular collisions. Instead of solving the Boltzmann equation with conventional finite difference or finite volume methods, particle methods are typically applied. Here, the fluid density is approximated by an ensemble of computational particles or point masses whose positions and velocities are evolved in a Lagrangian framework.
In the DSMC solution method, an appropriate number of particle pairs is selected per grid cell and time step. The selected particle pairs undergo a collision step. DSMC becomes expensive for small Kn as the number of explicitly treated binary collisions increases.
In the FP method on the other hand, the particle evolution is assumed to follow a continuous stochastic process. The process coefficients are selected consistently with the full Boltzmann collision operator. The FP collision operator is accurately integrable using large time steps in comparison to the small collision times that limit DSMC.
Since the two methods differ only in the treatment of the collision operator, a relatively simple hybrid FP-DSMC method can be devised. Here, if the total number of particles per grid cell is smaller than the number of colliding particles in a DSMC step, the FP collision operator is applied but otherwise DSMC is used.
Implementation
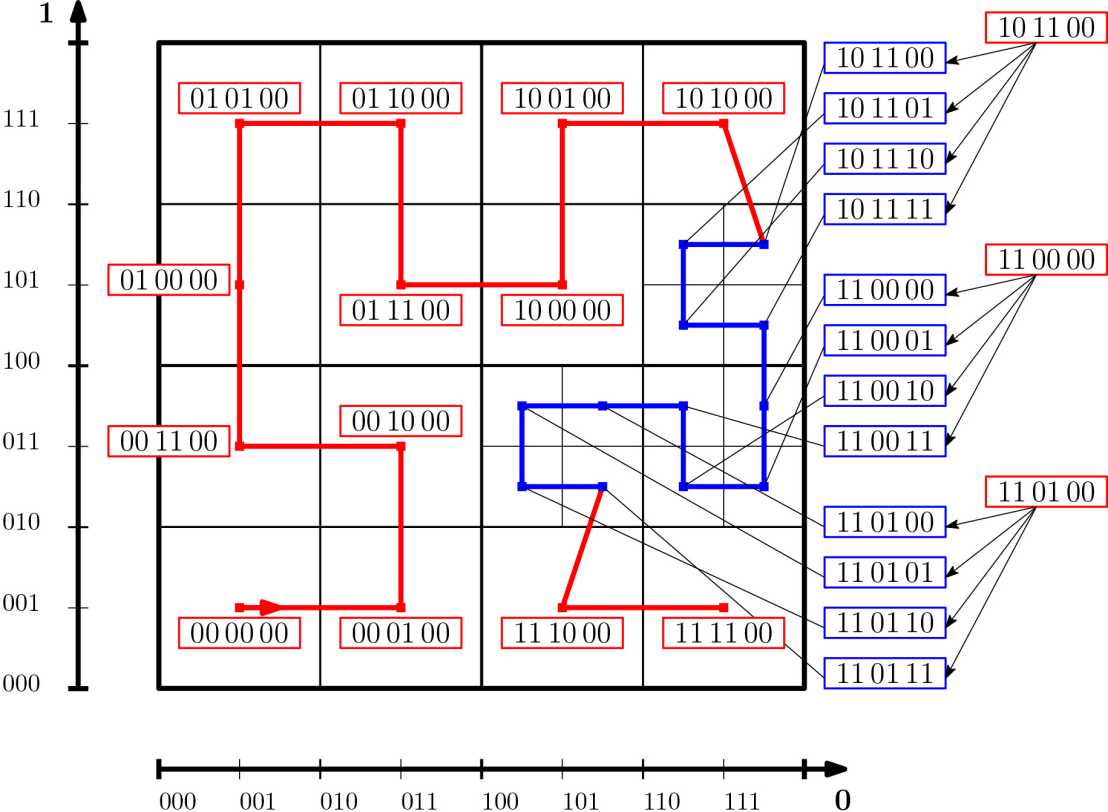
To exploit the full potential of parallel computing capabilities, an algorithm that distributes the particles evenly among the different processors is necessary. At the same time the communication overhead induced by particles crossing grid-cell boundaries between timesteps has to be kept at a minimum. In order to achieve these goals, space filling curves (SFC) are applied that promote proximity in physical as well as index space (computer memory). Furthermore, SFCs enable nesting of smaller cells in index space as adaptive mesh refinement (AMR) is applied (see figure). AMR is important in order to adaptively resolve variations in macroscopic properties such as mean flow velocity, density, temperature, etc.
Numerical Applications
We simulate hypersonic reentry flow over a generic planetary probe geometry (70 degree blunted cone flow). The simulation is run in parallel on 48 nodes, each using 4 cores (8 threads). The mesh is automatically refined at multiple time-instances at run time according to an estimate of the local equilibrium Knudsen number. The simulation is performed both using pure DSMC and using FP-DSMC, with the latter resulting in over 10 times faster simulations with excellent agreement to the DSMC reference runs. The figure shows a typical simulation result.
Source Code
The Eiger source code is available from the external page ETH Data Archive.